Definition 2.6.1.
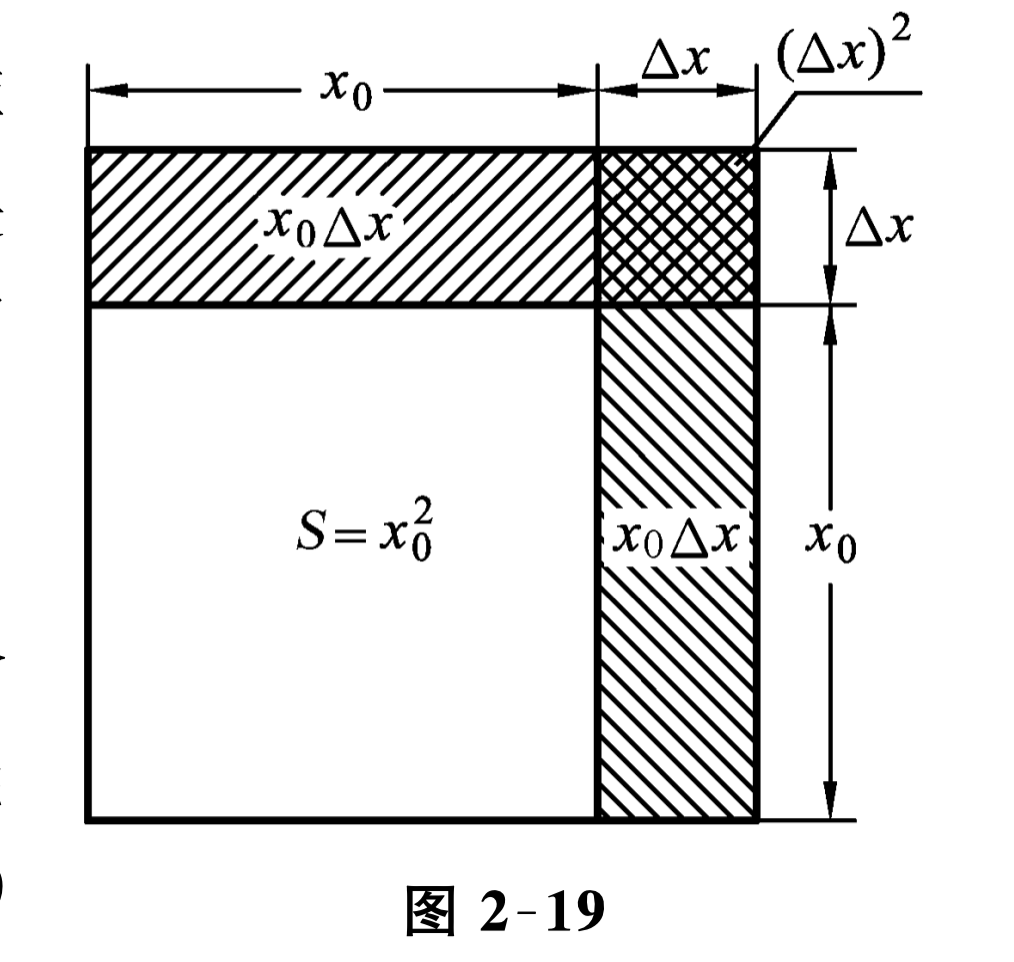
定义 设函数 \(y=f(x)\) 在点 \(x_{0}\) 的某邻域内有定义,若函数 \(y=f(x)\) 在点 \(x_{0}\) 的增量
\begin{equation*}
\Delta y=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)
\end{equation*}
可以表示成
\begin{equation}
\Delta y=A \Delta x+o(\Delta x)\tag{2.6.1}
\end{equation}
其中 \(A\) 是与 \(\Delta x\) 无关的常数,则称 \(y=f(x)\) 在点 \(x_{0}\) 可微, \(A \Delta x\) 称为 \(y=f(x)\) 在 \(x_{0}\) 的微分, 记作 \(\mathrm{d} y\text{,}\) 即
\begin{equation}
\mathrm{d} y=A \Delta x \text { 或 } \mathrm{d} f(x)=A \Delta x \text {. }\tag{2.6.2}
\end{equation}