Subsection 8.7.1 三角函数系的正交性及三角级数
先引人三角函数系: 函数列
\begin{equation}
1, \cos x, \sin x, \cos 2 x, \sin 2 x, \cdots, \cos n x, \sin n x, \cdots\tag{8.7.2}
\end{equation}
称为三角函数系. 容易看出, 三角级数
(8.7.1)就是将三角函数系
(8.7.2)中每一个函数分别乘以常数
\(\left(a_{0}, a_{1}, b_{1}, a_{2}, b_{2}, \cdots\right)\text{,}\) 然后相加组成的.
下面先介绍三角函数系的性质.
三角函数系
(8.7.2)中任何两个不同的函数的乘积在区间
\([-\pi, \pi]\) 上的积分等于零, 即
\begin{equation*}
\begin{aligned}
& \displaystyle \int_{-\pi}^{\pi} 1 \cdot \cos n x \mathrm{~d} x=0, \displaystyle \int_{-\pi}^{\pi} 1 \cdot \sin n x \mathrm{~d} x=0 \quad(n=1,2,3, \cdots), \\
& \displaystyle \int_{-\pi}^{\pi} \cos n x \cdot \sin k x \mathrm{~d} x=0 \quad(n, k=1,2,3, \cdots), \\
& \displaystyle \int_{-\pi}^{\pi} \cos n x \cdot \cos k x \mathrm{~d} x=0, \displaystyle \int_{-\pi}^{\pi} \sin n x \cdot \sin k x \mathrm{~d} x=0 \quad(n, k=1,2,3, \cdots, n \neq k) .
\end{aligned}
\end{equation*}
三角函数系
(8.7.2)中,同一个函数自身的乘积在区间
\([-\pi, \pi]\) 上的积分不等于零. 事实上,
\begin{equation*}
\begin{gathered}
\displaystyle \int_{-\pi}^{\pi} \cos ^{2} n x \mathrm{~d} x=\displaystyle \int_{-\pi}^{\pi} \sin ^{2} n x \mathrm{~d} x=\pi \quad(n=1,2,3, \cdots), \\
\displaystyle \int_{-\pi}^{\pi} 1 \mathrm{~d} x=2 \pi .
\end{gathered}
\end{equation*}
以上等式都可以通过计算定积分来加以验证 (具体证明留给读者).
这两个性质给出了三角函数系的正交性, 即三角函数系在区间 \([-\pi, \pi]\) 上是正交的.
在第 1 章中介绍过周期函数的概念,周期函数可以用来刻画生产实践和科学研究中的周期现象. 正弦函数是最简单的周期函数. 例如
\begin{equation*}
y=A \sin (\omega t+\varphi)
\end{equation*}
就是研究简单振动时得到的相应的数学模型, 其中 \(y\) 表示振动点的位置, \(t\) 表示时间, \(A\) 表示振幅, \(\omega\) 为角频率, \(\varphi\) 为初相.
在实际中, 人们所遇到的周期现象通常不会像正弦函数那么简单. 那么如何 深人研究复杂的非正弦的周期函数呢? 联系到前面学过的利用幂级数展开函数,并应用幂级数性质来研究函数的思路, 也可将一般的周期函数表示为简单的正弦函数组成的级数. 具体地说, 就是将周期为 \(T\left(=\frac{2 \pi}{\omega}\right)\) 的周期函数用一系列以 \(T\) 为周期的正弦函数 \(A_{n} \sin \left(n \omega t+\varphi_{n}\right)\) 组成的级数来表示它, 即
\begin{equation}
f(t)=A_{0}+\sum\limits_{n=1}^{\infty} A_{n} \sin \left(n \omega t+\varphi_{n}\right)\tag{8.7.3}
\end{equation}
其中 \(A_{0}, A_{n}, \varphi_{n}(n=1,2,3, \cdots)\) 都是与 \(t\) 无关的常数.
由三角公式可得
\begin{equation*}
A_{n} \sin \left(n \omega t+\varphi_{n}\right)=A_{n} \sin \varphi_{n} \cos n \omega t+A_{n} \cos \varphi_{n} \sin n \omega t,
\end{equation*}
并且令
\(\frac{a_{0}}{2}=A_{0}, a_{n}=A_{n} \sin \varphi_{n}, b_{n}=A_{n} \cos \varphi_{n}, \omega t=x\text{,}\) 则式
(8.7.3) 右端的级数就是三角级数
(8.7.1).
因此,现在要讨论的问题就变成以
\(2 \pi\) 为周期的函数如何展开成三角级数
(8.7.1).
Subsection 8.7.2 函数的傅里叶级数
要将函数
\(f(x)\) 展开成三角级数, 必须解决两个问题: (1) 什么样的函数可以展开为三角级数? (2) 三角级数
(8.7.1)中的系数
\(a_{0}, a_{n}, b_{n}(n=1,2,3, \cdots)\) 与函数
\(f(x)\) 是什么关系?
为此,先假设周期为 \(2 \pi\) 的函数 \(f(x)\) 可展开为三角级数:
\begin{equation}
f(x)=\frac{a_{0}}{2}+\sum\limits_{k=1}^{\infty}\left(a_{k} \cos k x+b_{k} \sin k x\right)\tag{8.7.4}
\end{equation}
并假定这个级数可以逐项积分.
对式
(8.7.4)两边从
\(-\pi\) 到
\(\pi\) 逐项积分, 得
\begin{equation*}
\displaystyle \int_{-\pi}^{\pi} f(x) \mathrm{d} x=\frac{a_{0}}{2} \displaystyle \int_{-\pi}^{\pi} \mathrm{d} x+\sum\limits_{k=1}^{\infty}\left(a_{k} \displaystyle \int_{-\pi}^{\pi} \cos k x \mathrm{~d} x+b_{k} \displaystyle \int_{-\pi}^{\pi} \sin k x \mathrm{~d} x\right) .
\end{equation*}
根据三角函数系
(8.7.2)的正交性, 等式右端除第一项外, 其余各项均为零, 所以
\begin{equation*}
\begin{aligned}
& \displaystyle \int_{-\pi}^{\pi} f(x) \mathrm{d} x=a_{0} \pi, \\
& a_{0}=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \mathrm{d} x .
\end{aligned}
\end{equation*}
为了求出
\(a_{n}\text{,}\)对式
(8.7.4)两边乘以
\(\cos n x\text{,}\) 再从
\(-\pi\) 到
\(\pi\) 积分, 得
\begin{equation*}
\begin{aligned}
& \displaystyle \int_{-\pi}^{\pi} f(x) \cos n x \mathrm{~d} x \\
= & \frac{a_{0}}{2} \displaystyle \int_{-\pi}^{\pi} \cos n x \mathrm{~d} x+\sum\limits_{k=1}^{\infty}\left(a_{k} \displaystyle \int_{-\pi}^{\pi} \cos k x \cos n x \mathrm{~d} x+b_{k} \displaystyle \int_{-\pi}^{\pi} \sin k x \cos n x \mathrm{~d} x\right) .
\end{aligned}
\end{equation*}
根据三角函数系
(8.7.2) 的正交性, 等式右端除
\(k=n\) 的一项外, 其余各项均为零,所以
\begin{equation*}
\displaystyle \int_{-\pi}^{\pi} f(x) \cos n x \mathrm{~d} x=a_{n} \displaystyle \int_{-\pi}^{\pi} \cos ^{2} n x \mathrm{~d} x=a_{n} \pi,
\end{equation*}
得
\begin{equation*}
a_{n}=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \cos n x \mathrm{~d} x \quad(n=1,2,3, \cdots) .
\end{equation*}
类似地,用
\(\sin n x\) 乘以式
(8.7.4)两边,再从
\(-\pi\) 到
\(\pi\) 逐项积分, 可得
\begin{equation*}
b_{n}=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \sin n x \mathrm{~d} x \quad(n=1,2,3, \cdots) .
\end{equation*}
由于当 \(n=0\) 时, \(a_{n}\) 的表达式正好给出 \(a_{0}\text{,}\) 因此, 已得结果可以合并写成
\begin{equation}
\begin{cases}a_{n}=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \cos n x \mathrm{~d} x & (n=0,1,2,3, \cdots), \\ b_{n}=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \sin n x \mathrm{~d} x & (n=1,2,3, \cdots) .\end{cases}\tag{8.7.5}
\end{equation}
如果公式
(8.7.5)中的积分都存在, 那么这时它们确定的系数
\(a_{0}, a_{1}, b_{1}, \cdots\) 叫做函数
\(f(x)\) 的傅里叶系数, 若三角级数
(8.7.1)中的系数
\(a_{0}, a_{1}, b_{1}, \cdots\) 满足条件
(8.7.5), 则称三角级数
(8.7.1)为函数
\(f(x)\) 的傅里叶级数.
Subsection 8.7.3 傅里叶级数的收敛性定理——狄利克雷(Dirichlet) 充分条件
到目前为止,一个函数的傅里叶级数完全是按形式作出的. 为了表明级数
(8.7.1)与生成它的函数
\(f(x)\) 的关系,通常用以下记号表示:
\begin{equation*}
f(x) \sim \frac{a_{0}}{2}+\sum\limits_{k=1}^{\infty}\left(a_{k} \cos k x+b_{k} \sin k x\right)
\end{equation*}
注意 这里不能写成等式, 只可用符号“~”表示“生成”.
下面给出傅里叶级数的一个收敛定理 (不加证明), 定理的条件是很宽松的,实际问题中的函数大都能满足.
Theorem 8.7.1.
定理 \(\mathbf{1}\) (狄利克雷 (Dirichlet) 充分条件) 设 \(f(x)\) 是周期为 \(2 \pi\) 的周期函数,若 \(f(x)\) 在 \([-\pi, \pi]\) 上只有有限多个第一类间断点和有限多个极值点, 在其他点连续,则 \(f(x)\) 的傅里叶级数收敛, 且有以下结论:
在连续点 \(x_{0}\text{,}\) 收敛于 \(f\left(x_{0}\right)\text{;}\)
在间断点 \(x_{0}\text{,}\) 收敛于 \(\frac{1}{2}\left[f\left(x_{0}-0\right)+f\left(x_{0}+0\right)\right]\text{;}\)
在 \([-\pi, \pi]\) 的端点处, 收敛于 \(\frac{1}{2}[f(\pi-0)+f(-\pi+0)]\text{.}\)
定理说明: 如果函数
\(f(x)\) 满足狄利克雷条件, 那么由式
(8.7.5)确定的傅里叶系数所构成的傅里叶级数
(8.7.1)在
\([-\pi, \pi]\) 上收敛, 并且
\begin{equation}
\begin{aligned}
& \frac{a_{0}}{2}+\sum\limits_{k=1}^{\infty}\left(a_{k} \cos k x+b_{k} \sin k x\right) \\
= & \begin{cases}f(x), & \text { 当 } x \text { 是 } f(x) \text { 的连续点时, } \\
\frac{f(x-0)+f(x+0)}{2}, & \text { 当 } x \text { 是 } f(x) \text { 的间断点时, } \\
\frac{f(\pi-0)+f(-\pi+0)}{2}, & \text { 当 } x= \pm \pi \text { 时. }\end{cases}
\end{aligned}\tag{8.7.6}
\end{equation}
若 \(f(x)\) 的图形如图 8-9a 所示, 则 \(f(x)\) 的傅里叶级数的和函数图形如图 8-9b 所示.
注意 \(f(x)\) 展开成傅里叶级数的条件中允许 \(f(x)\) 在 \([-\pi, \pi]\) 上有有限多个第一类间断点和有限多个极值点 (即函数不作无限次的振动). 这比函数 \(f(x)\) 展开成 \(x\) 的幂级数的条件要弱得多 (后者要求有连续的任意阶导数).
收敛定理中只给出了一个周期 \([-\pi, \pi]\) 上函数 \(f(x)\) 的三角函数展开式,因为函数 \(f(x)\) 和展开式都是周期函数, 所以所得结果也适用于 \([-\pi, \pi]\) 以外的一切点.
Example 8.7.2.
例 1 设 \(f(x)\) 是周期为 \(2 \pi\) 的周期函数, 它在 \([-\pi, \pi)\) 上的表达式为
\begin{equation*}
f(x)= \begin{cases}-1, & -\pi \leqslant x<0 \\ 1, & 0 \leqslant x<\pi\end{cases}
\end{equation*}
将 \(f(x)\) 展开成傅里叶级数.
Solution.
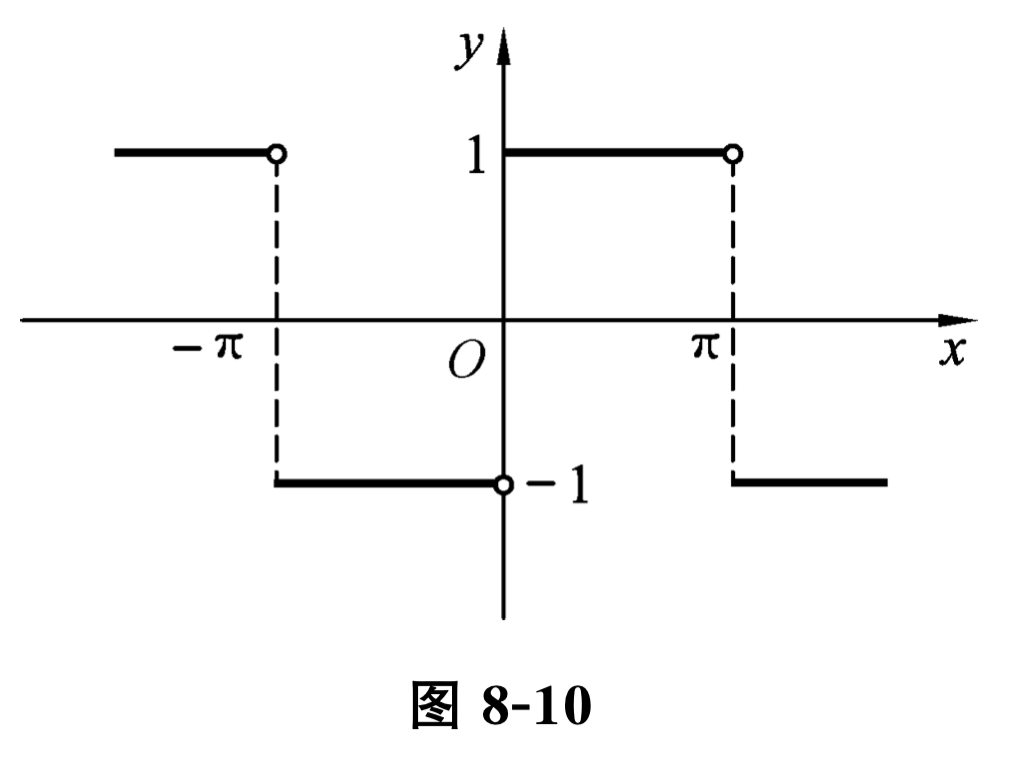
解 所给函数满足收敛定理的条件, 它在点 \(x=k \pi(k=0, \pm 1, \pm 2, \cdots)\) 处不连续, 在其他点处连续, 它的图形如图 8-10 所示. 由收敛定理可知 \(f(x)\) 展开成的傅里叶级数收敛, 并且当 \(x=k \pi\) 时级数收敛于 \(\frac{-1+1}{2}=\frac{1+(-1)}{2}=0\text{,}\) 当 \(x \neq k \pi\) 时级数收敛于 \(f(x)\text{,}\) 和函数的图形如图 8-11 所示.
计算傅里叶系数如下:
\begin{equation*}
\begin{aligned}
a_{n} & =\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \cos n x \mathrm{~d} x=\frac{1}{\pi} \displaystyle \int_{-\pi}^{0}(-1) \cos n x \mathrm{~d} x+\frac{1}{\pi} \displaystyle \int_{0}^{\pi} 1 \cdot \cos n x \mathrm{~d} x=0 \\
b_{n} & =\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \sin n x \mathrm{~d} x=\frac{1}{\pi} \displaystyle \int_{-\pi}^{0}(-1) \sin n x \mathrm{~d} x+\frac{1}{\pi} \displaystyle \int_{0}^{\pi} 1 \cdot \sin n x \mathrm{~d} x \\
& =\frac{1}{\pi}\left[\frac{\cos n x}{n}\right]_{-\pi}^{0}+\frac{1}{\pi}\left[-\frac{\cos n x}{n}\right]_{0}^{\pi}=\frac{1}{n \pi}(1-\cos n \pi-\cos n \pi+1) \\
& =\frac{2}{n \pi}\left[1-(-1)^{n}\right]= \begin{cases}\frac{4}{n \pi}, & n=1,3,5, \cdots, \\
0, & n=2,4,6, \cdots .\end{cases}
\end{aligned}
\end{equation*}
因此,
\begin{equation}
\frac{4}{\pi}\left[\sin x+\frac{1}{3} \sin 3 x+\cdots+\frac{1}{2 k-1} \sin (2 k-1) x+\cdots\right]= \begin{cases}f(x), & x \neq k \pi, \\ 0, & x=k \pi .\end{cases}\tag{8.7.7}
\end{equation}
如果把
Example 8.7.2中的函数理解为矩形波的波形函数 (周期
\(T=2 \pi\text{,}\)幅值
\(E=1\text{,}\)自变量
\(x\) 表示时间),那么上面展开式
(8.7.7) 表明: 矩形波是由一系列不同频率的正弦波叠加而成的.
一般地,可按下列步骤把周期为 \(2 \pi\) 的函数 \(f(x)\) 展开为傅里叶级数:
判断 \(f(x)\) 是否满足 Dirichlet 条件,并确定 \(f(x)\) 所有间断点. 此时,如果作出 \(y=f(x)\) 的图形,并结合图形进行判断,常能带来许多方便.
写出 \(f(x)\) 的傅里叶级数展开式,并注意这个展开式在哪些点成立.
Example 8.7.3.
例 2 设函数 \(f(x)\) 的周期为 \(2 \pi\text{,}\) 它在 \([-\pi, \pi)\) 上的表示式为
\begin{equation*}
f(x)= \begin{cases}0, & -\pi \leqslant x \leqslant 0 \\ x, & 0<x<\pi\end{cases}
\end{equation*}
将 \(f(x)\) 展开成傅里叶级数, 并作 \(f(x)\) 及其和函数的图形.
Solution.
解 注意 \(f(x)\) 在 \([-\pi, \pi)\) 上是分段函数,因此在 \([-\pi, \pi)\) 上的定积分应分段计算:
\begin{equation*}
\begin{aligned}
& a_{0}=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \mathrm{d} x=\frac{1}{\pi}\left[\displaystyle \int_{-\pi}^{0} f(x) \mathrm{d} x+\displaystyle \int_{0}^{\pi} f(x) \mathrm{d} x\right]=\frac{1}{\pi} \displaystyle \int_{0}^{\pi} x \mathrm{~d} x=\frac{\pi}{2}, \\
& a_{n}=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \cos n x \mathrm{~d} x=\frac{1}{\pi} \displaystyle \int_{0}^{\pi} x \cos n x \mathrm{~d} x \\
& =\frac{1}{\pi}\left(\left.x \cdot \frac{1}{n} \sin n x\right|_{0} ^{\pi}-\frac{1}{n} \displaystyle \int_{0}^{\pi} \sin n x \mathrm{~d} x\right) \\
& =\left.\frac{1}{\pi n^{2}} \cos n x\right|_{0} ^{\pi}=\frac{1}{\pi n^{2}}\left[(-1)^{n}-1\right],
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
b_{n} & =\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \sin n x \mathrm{~d} x=\frac{1}{\pi} \displaystyle \int_{0}^{\pi} x \sin n x \mathrm{~d} x \\
& =\frac{1}{\pi}\left[\left.x\left(-\frac{1}{n} \cos n x\right)\right|_{0} ^{\pi}+\frac{1}{n} \displaystyle \int_{0}^{\pi} \cos n x \mathrm{~d} x\right] \\
& =\frac{-1}{\pi n} \pi \cos n \pi=\frac{1}{n}(-1)^{n-1} .
\end{aligned}
\end{equation*}
所以,
\begin{equation}
\begin{aligned}
& \frac{\pi}{4}+\sum\limits_{n=1}^{\infty}\left\{\frac{1}{\pi n^{2}}\left[(-1)^{n}-1\right] \cos n x+\frac{1}{n}(-1)^{n-1} \sin n x\right\} \\
= & \left\{\begin{array}{ll}
f(x), & x \neq \pm(2 k+1) \pi, \\
\frac{\pi}{2}, & x= \pm(2 k+1) \pi
\end{array} \quad(k=0,1,2, \cdots) .\right.
\end{aligned}\tag{8.7.8}
\end{equation}
\(f(x)\) 的图形如图 8-12a 所示, \(f(x)\) 的傅里叶级数的和函数图形如图 8-12b 所示.
由该题的傅里叶级数还可以得到无理数 \(\pi\) 的平方的一个数项级数表示式.
\begin{equation*}
0=\frac{\pi}{4}+\frac{1}{\pi} \sum\limits_{n=1}^{\infty} \frac{1}{n^{2}}\left[(-1)^{n}-1\right],
\end{equation*}
由
\begin{equation*}
\begin{gathered}
\frac{1}{n^{2}}\left[(-1)^{n}-1\right]= \begin{cases}0, & n=2 k, \\
-\frac{2}{(2 k-1)^{2}}, & n=2 k-1,\end{cases}
\end{gathered}
\end{equation*}
得
\begin{equation*}
0=\frac{\pi}{4}-\frac{2}{\pi} \sum\limits_{k=1}^{\infty} \frac{1}{(2 k-1)^{2}},
\end{equation*}
于是得 \(\frac{\pi^{2}}{8}=\sum\limits_{k=1}^{\infty} \frac{1}{(2 k-1)^{2}}=1+\frac{1}{3^{2}}+\frac{1}{5^{2}}+\frac{1}{7^{2}}+\cdots+\frac{1}{(2 k+1)^{2}}+\cdots\text{.}\)
因为周期函数在任何长度为一周期的区间上, 其积分的数值相等, 所以,若周期为 \(2 \pi\) 的函数 \(f(x)\) 只在 \([0,2 \pi]\) 上给出表示式, 则计算傅里叶系数的公式为
\begin{equation}
\begin{cases}a_{n}=\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} f(x) \cos n x \mathrm{~d} x, & n=0,1,2,3, \cdots, \\ b_{n}=\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} f(x) \sin n x \mathrm{~d} x, & n=1,2,3, \cdots .\end{cases}\tag{8.7.9}
\end{equation}
另外,许多实际问题只要求将 \(f(x)\) 在区间 \([0,2 \pi)\) 上展开为傅里叶级数 (此时 \(f(x)\) 在这个区间外可能无定义,也可能有定义而无周期性), 为了在这一特定区间上展开,可以先将函数延拓为以 \(2 \pi\) 为周期的周期函数 (称为周期延拓)
\(F(x)=f(x), x \in[0,2 \pi)\text{,}\)
且
\begin{equation*}
F(x)=F(x+2 \pi), x \in(-\infty,+\infty) .
\end{equation*}
将 \(F(x)\) 展开成傅里叶级数, 然后限制 \(x\) 在 \([0,2 \pi)\) 上, 此时由于 \(F(x) \equiv f(x)\text{,}\) 由 \(F(x)\) 的傅里叶级数展开式就可以得到 \(f(x)\) 在区间 \([0,2 \pi)\) 上的傅里叶级数展开式.
Example 8.7.4.
例 3 将函数 \(f(x)=x(0 \leqslant x<2 \pi)\) 展开为傅里叶级数.
Solution.
解 这个函数在 \([0,2 \pi)\) 上有定义,将其周期开拓为以 \(2 \pi\) 为周期的函数, 由收敛定理可知, 当 \(x \in(0,2 \pi)\) 时,傅里叶级数收敛于 \(f(x)\text{,}\) 当 \(x=0\) 时级数收敛于 \(\frac{f(0)+f(2 \pi)}{2}=\pi\text{.}\)
计算傅里叶系数如下:
\begin{equation*}
\begin{aligned}
a_{0} & =\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} f(x) \mathrm{d} x=\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} x \mathrm{~d} x=2 \pi, \\
a_{n} & =\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} f(x) \cos n x \mathrm{~d} x=\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} x \cos n x \mathrm{~d} x \\
& \left.=\left.\frac{1}{\pi}\left[\left(x \cdot \frac{1}{n} \sin n x\right)\right)\right|_{0} ^{2 \pi}-\frac{1}{n} \displaystyle \int_{0}^{2 \pi} \sin n x \mathrm{~d} x\right]=0, \\
b_{n} & =\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} f(x) \sin n x \mathrm{~d} x=\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} x \sin n x \mathrm{~d} x \\
& =\frac{1}{\pi}\left[\left.x\left(-\frac{1}{n} \cos n x\right)\right|_{0} ^{2 \pi}+\frac{1}{n} \displaystyle \int_{0}^{2 \pi} \cos n x \mathrm{~d} x\right]=-\frac{2}{n} .
\end{aligned}
\end{equation*}
因此,
\begin{equation}
\pi-2 \sum\limits_{n=1}^{\infty} \frac{1}{n} \sin n x= \begin{cases}f(x), & 0<x<2 \pi, \\ \pi, & x=0 .\end{cases}\tag{8.7.10}
\end{equation}
Example 8.7.5.
例 4 将函数 \(f(x)=x^{2}(0<x<2 \pi)\) 展开成傅里叶级数并计算 \(\sum\limits_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}\text{.}\)
Solution.
解 见图 8-13, 所给函数在区间 (0, \(2 \pi)\) 内满足收敛定理的条件. 将它拓广到周期为 \(2 \pi\) 的周期函数后, 除了在 \(0, \pm 2 \pi\text{,}\) \(\pm 4 \pi, \cdots\) 外皆连续,因此拓广的周期函数在 \((0,2 \pi)\) 内收敛于 \(f(x)\text{.}\)
\begin{equation*}
\begin{aligned}
& a_{0}=\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} x^{2} \mathrm{~d} x=\frac{8}{3} \pi^{2} \\
& a_{n}=\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} x^{2} \cos n x \mathrm{~d} x=\frac{4}{n^{2}}, n=1,2, \cdots,
\end{aligned}
\end{equation*}
\begin{equation*}
b_{n}=\frac{1}{\pi} \displaystyle \int_{0}^{2 \pi} x^{2} \sin n x \mathrm{~d} x=-\frac{4 \pi}{n}, n=1,2, \cdots
\end{equation*}
所以
\begin{equation}
x^{2}=\frac{4}{3} \pi^{2}+4 \sum\limits_{n=1}^{\infty} \frac{1}{n^{2}} \cos n x-4 \pi \sum\limits_{n=1}^{\infty} \frac{1}{n} \sin n x \quad(0<x<2 \pi) .\tag{8.7.11}
\end{equation}
在式
(8.7.11) 两边, 令
\(x=\pi \in(0,2 \pi)\text{,}\)有
\begin{equation*}
\pi^{2}=\frac{4}{3} \pi^{2}+4 \sum\limits_{n=1}^{\infty} \frac{(-1)^{n}}{n^{2}},
\end{equation*}
由此得
\begin{equation*}
\sum\limits_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}=\frac{\pi^{2}}{12} .
\end{equation*}
Subsection 8.7.4 正弦级数与余弦级数
如果
\(f(x)\) 是周期为
\(2 \pi\) 的奇函数, 那么
\(f(x) \cos n x\) 是奇函数,
\(f(x) \sin n x\) 是偶函数, 由于傅里叶系数的计算公式
(8.7.5)是在对称区间上积分, 因此
\begin{equation}
\begin{cases}a_{n}=0, & n=0,1,2, \cdots, \\ b_{n}=\frac{2}{\pi} \displaystyle \int_{0}^{\pi} f(x) \sin n x \mathrm{~d} x, & n=1,2,3, \cdots .\end{cases}\tag{8.7.12}
\end{equation}
从而,
\begin{equation}
f(x) \sim \sum\limits_{n=1}^{\infty} b_{n} \sin n x\tag{8.7.13}
\end{equation}
即奇函数的傅里叶级数是只含正弦项的正弦级数.
如果 \(f(x)\) 是周期为 \(2 \pi\) 的偶函数, 此时 \(f(x) \cos n x\) 是偶函数, \(f(x) \sin n x\) 是奇函数, 于是
\begin{equation}
\begin{cases}a_{n}=\frac{2}{\pi} \displaystyle \int_{0}^{\pi} f(x) \cos n x \mathrm{~d} x, & n=0,1,2, \cdots, \\ b_{n}=0, & n=1,2,3, \cdots,\end{cases}\tag{8.7.14}
\end{equation}
则
\begin{equation}
f(x) \sim \frac{a_{0}}{2}+\sum\limits_{n=1}^{\infty} a_{n} \cos n x\tag{8.7.15}
\end{equation}
即偶函数的傅里叶级数是只含常数项和余弦项的余弦级数.
Example 8.7.6.
例 5 将函数 \(f(x)=x(-\pi \leqslant x<\pi)\) 展开为傅里叶级数.
Solution.
解 所给函数在 \([-\pi, \pi)\) 内满足收敛定理的条件. 将它拓广到周期为 \(2 \pi\) 的周期函数后, 除了在 \(x=(2 k+1) \pi(k=0, \pm 1, \pm 2, \cdots)\) 外皆连续, 由收敛定理可知,当 \(x \in(-\pi, \pi)\) 时,傅里叶级数收敛于 \(f(x)\text{,}\) 当 \(x=-\pi\) 时级数收敛于
\begin{equation*}
\frac{f(-\pi+0)+f(-\pi-0)}{2}=\frac{f(-\pi+0)+f(\pi-0)}{2}=\frac{-\pi+\pi}{2}=0
\end{equation*}
若不计
\(x=(2 k+1) \pi(k=0, \pm 1, \pm 2, \cdots)\text{,}\) 则函数
\(f(x)\) 是奇函数, 所以由公式
(8.7.12)有
\(a_{n}=0(n=0,1,2, \cdots)\text{,}\)而
\begin{equation*}
\begin{aligned}
b_{n} & =\frac{2}{\pi} \displaystyle \int_{0}^{\pi} f(x) \sin n x \mathrm{~d} x=\frac{2}{\pi} \displaystyle \int_{0}^{\pi} x \sin n x \mathrm{~d} x=\frac{2}{\pi}\left[-\frac{x \cos n x}{n}+\frac{\sin n x}{n^{2}}\right]_{0}^{\pi} \\
& =-\frac{2}{\pi} \cos n \pi=\frac{2}{\pi}(-1)^{n+1} \quad(n=1,2,3, \cdots) .
\end{aligned}
\end{equation*}
所以
\(2\left[\sin x-\frac{1}{2} \sin 2 x+\frac{1}{3} \sin 3 x-\cdots+\frac{(-1)^{n+1}}{n} \sin n x+\cdots\right]= \begin{cases}f(x), & -\pi<x<\pi, \\ 0 & x=-\pi .\end{cases}\)
在实际应用中,有时还需要把定义在区间 \([0, \pi]\) 上的函数 \(f(x)\) 展开成正弦级数或余弦级数. 根据前面讨论的结论, 这类问题可以按如下方法解决: 拓展函数 \(f(x)\) 的定义到区间 \((-\pi, \pi]\text{,}\) 得到函数 \(F(x)\text{,}\) 使得: (1) 函数 \(F(x)\) 在区间 \((-\pi, \pi)\)上为奇函数 (偶函数); (2) 在区间 \((0, \pi]\) 上 \(F(x) \equiv f(x)\text{,}\) 这种拓广函数定义域的过程称为奇延拓 (偶延拓).
具体可以采用以下方法:
Subsubsection 8.7.4.1 奇延拓
将 \(f(x)\) 延拓成 \((-\pi, \pi]\) 上的奇函数 \(F(x)\) :
\begin{equation*}
F(x)= \begin{cases}f(x), & x \in[0, \pi], \\ -f(-x), & x \in(-\pi, 0) .\end{cases}
\end{equation*}
如图 8-14a 所示, 于是 \(f(x)\) 在 \([0, \pi]\) 上可展开为正弦级数:
\begin{equation*}
f(x) \sim \sum\limits_{n=1}^{\infty} b_{n} \sin n x, \quad x \in[0, \pi]
\end{equation*}
其中 \(b_{n}=\frac{2}{\pi} \displaystyle \int_{0}^{\pi} f(x) \sin n x \mathrm{~d} x\text{.}\)
Subsubsection 8.7.4.2 偶延拓
将 \(f(x)\) 延拓成 \((-\pi, \pi]\) 上的偶函数 \(F(x)\) :
\begin{equation*}
F(x)= \begin{cases}f(x), & x \in[0, \pi], \\ f(-x), & x \in(-\pi, 0) .\end{cases}
\end{equation*}
如图 8-14b 所示, \(f(x)\) 在 \([0, \pi]\) 上可展开为余弦级数.
\begin{equation*}
f(x) \sim \frac{a_{0}}{2}+\sum\limits_{n=1}^{\infty} a_{n} \cos n x, x \in[0, \pi],
\end{equation*}
其中 \(a_{0}=\frac{2}{\pi} \displaystyle \int_{0}^{\pi} f(x) \mathrm{d} x, a_{n}=\frac{2}{\pi} \displaystyle \int_{0}^{\pi} f(x) \cos n x \mathrm{~d} x\text{.}\)
因此,仅在 \([0, \pi]\) 上有定义的函数, 既可以展开成正弦级数, 又可以展开成余弦级数, 其傅里叶级数是不唯一的.
Example 8.7.7.
例 6 设 \(f(x)=x+1, x \in[0, \pi]\text{.}\)
将 \(f(x)\) 作奇延拓, 求 \(f(x)\) 在 \([0, \pi]\) 上的正弦级数,
将 \(f(x)\) 作偶延拓, 求 \(f(x)\) 在 \([0, \pi]\) 上的余弦级数.
Solution.
解 先作奇延拓图和偶延拓图,如图 8-15a,b 所示.
\begin{equation*}
\begin{aligned}
b_{n} & =\frac{2}{\pi} \displaystyle \int_{0}^{\pi} f(x) \sin n x \mathrm{~d} x=\frac{2}{\pi} \displaystyle \int_{0}^{\pi}(x+1) \sin n x \mathrm{~d} x \\
& =\frac{2}{\pi}\left[-\frac{(x+1) \cos n x}{n}+\frac{\sin n x}{n^{2}}\right]_{0}^{\pi} \\
& =\frac{2}{\pi}[1-(\pi+1) \cos n \pi]= \begin{cases}\frac{2}{\pi} \cdot \frac{\pi+2}{n}, & n=1,3,5, \cdots, \\
-\frac{2}{\pi}, & n=2,4,6, \cdots .\end{cases}
\end{aligned}
\end{equation*}
于是
\(\frac{2}{\pi}\left[(\pi+2) \sin x-\frac{\pi}{2} \sin 2 x+\frac{1}{3}(\pi+2) \sin 3 x-\frac{1}{4} \sin 4 x+\cdots\right]= \begin{cases}x+1, & 0<x<\pi, \\ 0, & x=0, \pi .\end{cases}\)
\begin{equation*}
a_{0}=\frac{2}{\pi} \displaystyle \int_{0}^{\pi}(x+1) \mathrm{d} x=\frac{2}{\pi}\left[\frac{x^{2}}{2}+x\right]_{0}^{\pi}=\pi+2 ;
\end{equation*}
\begin{equation*}
\begin{aligned}
& \begin{aligned}
a_{n} & =\frac{2}{\pi} \displaystyle \int_{0}^{\pi}(x+1) \cos n x \mathrm{~d} x=\frac{2}{\pi}\left[\frac{(x+1) \sin n x}{n}+\frac{\cos n x}{n^{2}}\right]_{0}^{\pi} \\
& =\frac{2}{n^{2} \pi}(\cos n \pi-1)=\left\{\begin{array}{cc}
0, & n=2,4,6, \cdots, \\
-\frac{4}{n^{2} \pi}, & n=1,3,5, \cdots .
\end{array}\right. \\
\text { 故 } x+1 & =\frac{\pi}{2}+1-\frac{4}{\pi} \sum\limits_{k=1}^{\infty} \frac{1}{(2 k-1)^{2}} \cos (2 k-1) x, x \in[0, \pi] .
\end{aligned}
\end{aligned}
\end{equation*}
Subsection 8.7.5 一般周期函数的傅里叶级数
到目前为止,所讨论的都是以 \(2 \pi\) 为周期的周期函数的傅里叶级数展开,事实上,在实际问题中常常遇到的周期函数的周期不一定是 \(2 \pi\text{.}\) 因此,这里将讨论一般周期函数的傅里叶级数.
假设函数
\(f(x)\) 是为
\(2 l\) 周期的周期函数, 并假设
\(f(x)\) 在一个周期内
\([-l, l]\) (从而也在每个周期内) 满足收敛定理
Theorem 8.7.1的条件. 现在令
\(F(t)=f\left(\frac{l}{\pi} t\right)\text{,}\) 则
\(F(t)\) 就是以
\(2 \pi\) 为周期的周期函数,在一个周期内也满足收敛定理
Theorem 8.7.1的条件, 从而
\(F(t)\) 的傅里叶级数收敛, 而
\begin{equation}
F(t) \sim \frac{a_{0}}{2}+\sum\limits_{n=1}^{\infty}\left(a_{n} \cos n t+b_{n} \sin n t\right)\tag{8.7.16}
\end{equation}
\begin{equation*}
a_{n}=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} F(t) \cos n t \mathrm{~d} t=\frac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f\left(\frac{l}{\pi} t\right) \cos n t \mathrm{~d} t
\end{equation*}
作积分变量替换 \(t=\frac{\pi}{l} x\text{,}\) 得
\begin{equation}
a_{n}=\frac{1}{l} \displaystyle \int_{-l}^{l} f(x) \cos \frac{n \pi}{l} x \mathrm{~d} x\tag{8.7.17}
\end{equation}
同理得
\begin{equation}
b_{n}=\frac{1}{l} \displaystyle \int_{-l}^{l} f(x) \sin \frac{n \pi}{l} x \mathrm{~d} x\tag{8.7.18}
\end{equation}
因为
\(f(x)=F\left(\frac{\pi}{l} x\right)\text{,}\) 所以令
\(t=\frac{\pi}{l} x\text{,}\) 根据式
(8.7.16), 由
Theorem 8.7.1 就可得到下面定理.
Theorem 8.7.8.
定理 2 设 \(f(x)\) 是周期为 \(2 l\) 的周期函数,若 \(f(x)\) 在 \([-l, l]\) 上只有有限多个第一类间断点和有限多个极值点, 在其他点连续, 则 \(f(x)\) 的傅里叶级数
\begin{equation}
\frac{a_{0}}{2}+\sum\limits_{n=1}^{\infty}\left(a_{n} \cos \frac{n \pi x}{l}+b_{n} \sin \frac{n \pi x}{l}\right)\tag{8.7.19}
\end{equation}
收敛,其中系数
\(a_{0}, a_{n}, b_{n},(n=1,2,3, \cdots)\) 由公式
(8.7.17) 和
(8.7.18) 确定, 且有等式
\begin{equation}
\begin{aligned}
& \frac{a_{0}}{2}+\sum\limits_{n=1}^{\infty}\left(a_{n} \cos \frac{n \pi x}{l}+b_{n} \sin \frac{n \pi x}{l}\right) \\
= & \begin{cases}f(x), & \text { 当 } x \text { 是 } f(x) \text { 的连续点时, } \\
\frac{f(x-0)+f(x+0)}{2}, & \text { 当 } x \text { 是 } f(x) \text { 的间断点时, } \\
\frac{f(l-0)+f(-l+0)}{2}, & \text { 当 } x= \pm l \text { 时. }\end{cases}
\end{aligned}\tag{8.7.20}
\end{equation}
注意 当
\(f(x)\) 是奇函数 (或偶函数) 时, 仍然有
\(a_{n}=0, n=0,1,2, \cdots\) (或
\(b_{n}=0\text{,}\) \(n=1,2,3, \cdots)\text{,}\) 因此它的傅里叶级数
(8.7.19)仍然为正弦级数 (或余弦级数).
Example 8.7.9.
例 7 设 \(f(x)\) 是周期为 6 的周期函数, 它在 \([-3,3)\) 内的表示式为
\begin{equation*}
f(x)= \begin{cases}-1, & -3 \leqslant x<0 \\ 1, & 0 \leqslant x<3\end{cases}
\end{equation*}
将 \(f(x)\) 展开为傅里叶级数, 并作 \(f(x)\) 及其傅里叶级数的和函数图形.
Solution.
解 \(f(x)\) 是周期奇函数, 其图形如图 8-16 所示. 展开为正弦傅里叶级数, 其系数为
\begin{equation*}
\begin{aligned}
a_{0} & =0, a_{n}=0, \\
b_{n} & =\frac{2}{3} \displaystyle \int_{0}^{3} f(x) \sin \frac{n \pi}{3} x \mathrm{~d} x=\frac{2}{3} \displaystyle \int_{0}^{3} 1 \cdot \sin \frac{n \pi}{3} x \mathrm{~d} x \\
& =-\left.\frac{2}{3} \cdot \frac{3}{n \pi} \cos \frac{n \pi}{3} x\right|_{0} ^{3}=-\frac{2}{n \pi}(\cos n \pi-1) \\
& =-\frac{2}{n \pi}\left[(-1)^{n}-1\right)=\left\{\begin{array}{ll}
0, & n=2 k, \\
\frac{4}{\pi(2 k-1)}, & n=2 k-1
\end{array}(k=1,2,3, \cdots) .\right.
\end{aligned}
\end{equation*}
于是得 \(f(x)\) 的正弦傅里叶级数为
\begin{equation*}
\begin{aligned}
& f(x) \sim \frac{4}{\pi} \sum\limits_{k=1}^{\infty} \frac{1}{2 k-1} \sin \frac{(2 k-1) \pi}{3} x \\
= & \left\{\begin{array}{ll}
f(x), & x \neq \pm 3 k, \\
0, & x= \pm 3 k
\end{array} \quad(k=0,1,2, \cdots) .\right.
\end{aligned}
\end{equation*}
对于仅在 \([0, l]\) 上有定义的函数 \(f(x)\text{,}\) 与前面
仅定义在 \([0, \pi]\) 上的函数类似,一般可以通过奇延拓或偶延拓,把函数扩展成周期为 \(2 l\) 的奇函数或偶函数, 从而其生成的傅里叶级数就是正弦函数或余弦函数.
Example 8.7.10.
例 8 设 \(f(x)=x, x \in[0, l]\text{.}\)
将 \(f(x)\) 作奇延拓, 求 \(f(x)\) 在 \([0, l]\) 上的正弦级数,
将 \(f(x)\) 作偶延拓, 求 \(f(x)\) 在 \([0, l]\) 上的余弦级数.
Solution.
解 先作奇延拓图和偶延拓图,如图 8-18 所示.
(1)当 \(f(x)\) 作奇延拓后, \(a_{n}=0, n=0,1,2, \cdots\text{,}\) 且
\begin{equation*}
\begin{aligned}
b_{n} & =\frac{2}{l} \displaystyle \int_{0}^{l} x \sin \frac{n \pi}{l} x \mathrm{~d} x=-\frac{2}{l} \cdot \frac{l}{n \pi} \displaystyle \int_{0}^{l} x \mathrm{~d} \cos \frac{n \pi}{l} x \\
& =-\frac{2}{n \pi}\left(\left.x \cos \frac{n \pi}{l} x\right|_{0} ^{l}-\displaystyle \int_{0}^{l} \cos \frac{n \pi}{l} x \mathrm{~d} x\right)=\frac{2 l}{\pi n}(-1)^{n-1},
\end{aligned}
\end{equation*}
故
\begin{equation*}
\frac{2 l}{\pi} \sum\limits_{n=1}^{\infty} \frac{(-1)^{n-1}}{n} \sin \frac{n \pi}{l} x= \begin{cases}x, & x \in[0, l), \\ 0, & x=l .\end{cases}
\end{equation*}
(2) 当 \(f(x)\) 作偶延拓后, \(b_{n}=0, n=1,2,3, \cdots\text{,}\) 且
\begin{equation*}
\begin{gathered}
a_{0}=\frac{2}{l} \displaystyle \int_{0}^{l} x \mathrm{~d} x=l, \\
a_{n}=\frac{2}{l} \displaystyle \int_{0}^{l} x \cos \frac{n \pi}{l} x \mathrm{~d} x=\frac{2}{l} \cdot \frac{l}{n \pi} \displaystyle \int_{0}^{l} x \mathrm{~d} \sin \frac{n \pi}{l} x \\
=\frac{2}{n \pi}\left(\left.x \sin \frac{n \pi}{l} x\right|_{0} ^{l}-\displaystyle \int_{0}^{l} \sin \frac{n \pi}{l} x \mathrm{~d} x\right) \\
=\frac{2 l}{n^{2} \pi^{2}}\left[(-1)^{n}-1\right]= \begin{cases}0, & n=2 k, \\
-\frac{4 l}{\pi^{2}(2 k-1)^{2}}, & n=2 k-1 .\end{cases}
\end{gathered}
\end{equation*}
故
\begin{equation*}
x=\frac{l}{2}-\frac{4 l}{\pi^{2}} \sum\limits_{k=1}^{\infty} \frac{1}{(2 k-1)^{2}} \cos \frac{(2 k-1) \pi}{l} x, x \in[0, l] .
\end{equation*}
Subsection 8.7.6 *傅里叶级数的复数形式
利用8.5.4 介绍的欧拉 (Euler) 公式
(8.5.14), 可以很容易地写出傅里叶级数的复数形式.
设 \(f(x)\) 是周期为 \(2 l\) 的实变量函数, 它的傅里叶级数为
\begin{equation}
\frac{a_{0}}{2}+\sum\limits_{n=1}^{\infty}\left(a_{n} \cos \frac{n \pi x}{l}+b_{n} \sin \frac{n \pi x}{l}\right)\tag{8.7.21}
\end{equation}
其中系数的计算,由下式给出:
\begin{equation}
\begin{cases}a_{n}=\frac{1}{l} \displaystyle \int_{-l}^{l} f(x) \cos \frac{n \pi}{l} x \mathrm{~d} x \quad(n=0,1,2, \cdots), \\ b_{n}=\frac{1}{l} \displaystyle \int_{-l}^{l} f(x) \sin \frac{n \pi}{l} x \mathrm{~d} x \quad(n=1,2,3, \cdots) .\end{cases}\tag{8.7.22}
\end{equation}
由欧拉公式 \(\cos t=\frac{\mathrm{e}^{\mathrm{i} t}+\mathrm{e}^{-\mathrm{i} t}}{2}, \sin t=\frac{\mathrm{e}^{\mathrm{i} t}-\mathrm{e}^{-\mathrm{i} t}}{2 \mathrm{i}}\text{,}\)
\begin{equation}
\begin{aligned}
& \frac{a_{0}}{2}+\sum\limits_{n=1}^{\infty}\left[\frac{a_{n}}{2}\left(\mathrm{e}^{\frac{n \pi x}{l}}+\mathrm{e}^{-\mathrm{i} \frac{n \pi x}{l}}\right)-\frac{\mathrm{i} b_{n}}{2}\left(\mathrm{e}^{\mathrm{i} \frac{n \pi x}{l}}-\mathrm{e}^{-\mathrm{i} \frac{n \pi x}{l}}\right)\right] \\
= & \frac{a_{0}}{2}+\sum\limits_{n=1}^{\infty}\left(\frac{a_{n}-\mathrm{i} b_{n}}{2} \mathrm{e}^{\mathrm{i} \frac{n \pi x}{l}}+\frac{a_{n}+\mathrm{i} b_{n}}{2} \mathrm{e}^{-\mathrm{i} \frac{n \pi x}{l}}\right) .
\end{aligned}\tag{8.7.23}
\end{equation}
若记
\begin{equation}
\quad \frac{a_{0}}{2}=C_{0}, \frac{a_{n}-\mathrm{i} b_{n}}{2}=C_{n}, \frac{a_{n}+\mathrm{i} b_{n}}{2}=C_{-n} \quad(n=1,2,3, \cdots)\text{,}\tag{8.7.24}
\end{equation}
\begin{equation*}
C_{0}+\sum\limits_{n=1}^{\infty}\left(C_{n} \mathrm{e}^{\mathrm{i} \frac{n \pi x}{l}}+C_{-n} \mathrm{e}^{\mathrm{i} \frac{-n \pi x}{l}}\right)=\left(C_{n} \mathrm{e}^{\mathrm{i} \frac{n \pi x}{l}}\right)_{n=0}+\sum\limits_{n=1}^{\infty}\left(C_{n} \mathrm{e}^{\mathrm{i} \frac{n \pi x}{l}}+C_{-n} \mathrm{e}^{\mathrm{i} \frac{-n \pi x}{l}}\right),
\end{equation*}
即得傅里叶级数的复数形式为
\begin{equation}
\sum\limits_{n=-\infty}^{\infty} C_{n} \mathrm{e}^{\frac{i n \pi x}{l}}\text{.}\tag{8.7.25}
\end{equation}
\begin{equation*}
\begin{gathered}
C_{0}=\frac{a_{0}}{2}=\frac{1}{2 l} \displaystyle \int_{-l}^{l} f(x) \mathrm{d} x ; \\
C_{n}=\frac{a_{n}-\mathrm{i} b_{n}}{2}=\frac{1}{2 l} \displaystyle \int_{-l}^{l} f(x)\left(\cos \frac{n \pi x}{l}-\mathrm{i} \sin \frac{n \pi x}{l}\right) \mathrm{d} x \\
=\frac{1}{2 l} \displaystyle \int_{-l}^{l} f(x) \mathrm{e}^{-\mathrm{i} \frac{n \pi x}{l}} \mathrm{~d} x \quad(n=1,2,3, \cdots) ; \\
C_{-n}=\frac{a_{n}+\mathrm{i} b_{n}}{2}=\frac{1}{2 l} \displaystyle \int_{-l}^{l} f(x) \mathrm{e}^{\mathrm{i} \frac{n \pi x}{l}} \mathrm{~d} x \quad(n=1,2,3, \cdots) .
\end{gathered}
\end{equation*}
将已得的结果合并写为
\begin{equation}
C_{n}=\frac{1}{2 l} \displaystyle \int_{-l}^{l} f(x) \mathrm{e}^{-i \frac{n \pi x}{l}} \mathrm{~d} x \quad(n=0, \pm 1, \pm 2, \cdots),\tag{8.7.26}
\end{equation}
这就是傅里叶系数的复数形式.
Example 8.7.11.
例 9 把宽为 \(\tau\) 、高为 \(h\) 、周期为 \(T\) 的矩形波 (见图 8-19) 展开成复数形式的傅里叶级数.
Solution.
解 在一个周期 \(\left[-\frac{T}{2}, \frac{T}{2}\right]\) 内矩形波的函数表达式为
\begin{equation*}
u(t)= \begin{cases}0, & -\frac{T}{2} \leqslant t<-\frac{\tau}{2}, \\ h, & -\frac{\tau}{2} \leqslant t<\frac{\tau}{2}, \\ 0, & \frac{\tau}{2} \leqslant t<\frac{T}{2} .\end{cases}
\end{equation*}
根据欧拉公式 \(\mathrm{e}^{-\mathrm{i} \alpha x}=\cos \alpha x-\mathrm{i} \sin \alpha x\text{,}\) 当 \(\alpha \neq 0\) 时,有
\begin{equation*}
\begin{aligned}
\displaystyle \int \mathrm{e}^{-\mathrm{i} \alpha x} \mathrm{~d} x & =\displaystyle \int(\cos \alpha-\mathrm{i} \sin \alpha x) \mathrm{d} x=\displaystyle \int \cos \alpha x \mathrm{~d} x-\mathrm{i} \displaystyle \int \sin \mathrm{d} x \mathrm{~d} x \\
& =\frac{\sin \alpha x}{\alpha}+\mathrm{i} \frac{\cos \alpha x}{\alpha}+C=-\frac{1}{\mathrm{i} \alpha}(\cos \alpha x-\mathrm{i} \sin \alpha x)+C \\
& =\frac{1}{-\mathrm{i} \alpha} \mathrm{e}^{-\mathrm{i} \alpha x}+C,
\end{aligned}
\end{equation*}
所以
\begin{equation*}
\begin{aligned}
& C_{n}= \frac{1}{T} \displaystyle \int_{-\frac{T}{2}}^{\frac{T}{2}} u(t) \mathrm{e}^{-\mathrm{i} \frac{2 n \pi t}{T}} \mathrm{~d} t=\frac{1}{T} \displaystyle \int_{-\frac{\tau}{2}}^{\frac{\tau}{2}} h \mathrm{e}^{-\mathrm{i} \frac{2 n \pi t}{T}} \mathrm{~d} t \\
&= \frac{h}{T}\left[\frac{-T}{2 n \pi \mathrm{i}} \mathrm{e}^{-\mathrm{i} \frac{2 n \pi t}{T}}\right]_{-\frac{\tau}{2}}^{\frac{\tau}{2}}=\frac{h}{n \pi} \sin \frac{n \pi \tau}{T} \quad(n= \pm 1, \pm 2, \cdots), \\
& C_{0}=\frac{1}{T} \displaystyle \int_{-\frac{T}{2}}^{\frac{T}{2}} u(t) \mathrm{d} t=\frac{1}{T} \displaystyle \int_{-\frac{\tau}{2}}^{\frac{\tau}{2}} h \mathrm{~d} t=\frac{h \tau}{T} .
\end{aligned}
\end{equation*}
\(u(t)=\frac{h \tau}{T}+\frac{h}{\pi} \sum\limits_{\substack{n=-\infty \\ n \neq 0}}^{\infty} \frac{1}{n} \sin \frac{n \pi \tau}{T} \mathrm{e}^{\mathrm{i} \frac{2 n \pi t}{T}} \quad\left(-\infty<t<+\infty ; t \neq \pm \frac{\tau}{2}, \pm \frac{\tau}{2} \pm T, \cdots\right)\text{.}\)