Subsection 5.1.1 原函数
实践中经常要考虑如下类型的问题: 已知一个函数 \(f(x)\) 的导数为 \(f^{\prime}(x)\text{,}\) 要求 \(f(x)\text{.}\) 例如, 已知曲线 \(y=f(x)\) 上任一点 \((x, y)\) 处的切线斜率为 \(2 x\text{,}\) 如何求该曲线方程? 即求满足 \(f^{\prime}(x)=2 x\) 的函数 \(y=f(x)\text{.}\) 这类问题称为找 \(f^{\prime}(x)\) 的原函数. 为此,引人原函数的概念.
Definition 5.1.1.
定义 1 若在区间 \(I\) 上, 可导函数 \(F(x)\) 的导函数为 \(f(x)\text{,}\) 即对任意的 \(x \in I\text{,}\) 都有 \(F^{\prime}(x)=f(x)\) 或 \(\mathrm{d} F(x)=f(x) \mathrm{d} x\text{,}\) 则称函数 \(F(x)\) 是 \(f(x)\) 在区间 \(I\)上的一个原函数.
例如, 因为在 \((-\infty,+\infty)\) 内 \(\left(x^{2}\right)^{\prime}=2 x\text{,}\) 所以 \(x^{2}\) 是 \(2 x\) 在 \((-\infty,+\infty)\) 内的一 个原函数. 又如, 在 \(x \in(0,+\infty)\) 内,\((\sqrt{x})^{\prime}=\frac{1}{2 \sqrt{x}}\text{,}\) 所以 \(\sqrt{x}\) 是 \(\frac{1}{2 \sqrt{x}}\) 在 \((0,+\infty)\) 内的一个原函数. 什么样的函数存在原函数呢?
Theorem 5.1.2.
定理 1 (原函数存在定理) 若函数 \(f(x)\) 在区间 \(I\) 上连续,则在区间 \(I\) 上存在可导函数 \(F(x)\text{,}\) 使对任意的 \(x \in I\) 都有 \(F^{\prime}(x)=f(x)\text{.}\) 即任何一个在区间 \(I\) 上连续的函数,在区间 \(I\) 上都存在原函数.
由于初等函数在其定义区间内都是连续的,因而初等函数在其定义域内都存在原函数. 那么 \(f(x)\) 的原函数是否唯一呢? 回答是不唯一的. 由原函数的定义知,若 \(F^{\prime}(x)=f(x)\text{,}\) 则对任意常数 \(C\) 均有: \([F(x)+C]^{\prime}=f(x)\text{,}\) 可见当 \(F(x)\) 是 \(f(x)\) 的一个原函数时, \(F(x)+C\) 也是 \(f(x)\) 的一个原函数, 所以若已知函数 \(f(x)\)存在原函数,那么 \(f(x)\) 就有无穷多个原函数.
Theorem 5.1.3.
定理 2 若 \(F(x)\) 是函数 \(f(x)\) 的一个原函数,则函数 \(f(x)\) 有无限多个原函数,且其任何原函数均可表示成 \(F(x)+C\) 的形式 ( \(C\) 为任意常数).
Proof.
证 设 \(\Phi(x)\) 是函数 \(f(x)\) 的任意一个原函数,并令
\begin{equation*}
y=\Phi(x)-F(x),
\end{equation*}
\begin{equation*}
\begin{array}{ll}
\text { 由于 } & F^{\prime}(x)=f(x), \Phi^{\prime}(x)=f(x), \\
\text { 所以 } & y^{\prime}=\Phi^{\prime}(x)-F^{\prime}(x)=f(x)-f(x) \equiv 0 . \\
\text { 于是 } & \Phi(x)-F(x)=C \text { 或 } \Phi(x)=F(x)+C .
\end{array}
\end{equation*}
Subsection 5.1.2 不定积分的概念
Definition 5.1.4.
定义 2 在区间 \(I\) 上,函数 \(f(x)\) 的带有任意常数项的原函数称为 \(f(x)\) (或 \(f(x) \mathrm{d} x)\) 在区间 \(I\) 上的不定积分, 记作 \(\displaystyle \int f(x) \mathrm{d} x\text{,}\) 即
\begin{equation*}
\displaystyle \int f(x) \mathrm{d} x=F(x)+C,
\end{equation*}
其中 \(C\) 为任意常数, \(F(x)\) 是函数 \(f(x)\) 的一个原函数, \(f(x)\) 称为被积函数, \(f(x) \mathrm{d} x\) 称为被积表达式, \(\displaystyle \int\) 称为积分号, \(x\) 称为积分变量.
由此可见, 一个函数的不定积分不是一个确定的数, 也不是一个函数, 而是一个函数族. 例如, 因为 \((\sin x)^{\prime}=\cos x\text{,}\) 则 \(\displaystyle \int \cos x \mathrm{~d} x=\sin x+C\text{;}\) 又因为 \(\left(x^{2}\right)^{\prime}=2 x\text{,}\) 则 \(\displaystyle \int 2 x \mathrm{~d} x=x^{2}+C\text{.}\) 下面阐述原函数与不定积分的几何意义. 设 \(F(x)\) 是 \(f(x)\) 的一个原函数, \(y=F(x)\) 在平面上表示一条曲线,该曲线称为 \(f(x)\) 的积分曲线. 而 \(\displaystyle \int f(x) \mathrm{d} x=F(x)+C\) 表示一族曲线, 它是由 \(y=F(x)\) 沿 \(y\) 轴平移所得, 其中任一条曲线在具有同一横坐标 \(x\) 点处切线的斜率都等于 \(f(x)\text{.}\) 在实际问题中, 有时要求 \(f(x)\) 通过点 \(\left(x_{0}, y_{0}\right)\) 的积分曲线, 此时有 \(y_{0}=\) \(F\left(x_{0}\right)+C\text{,}\) 则 \(C=y_{0}-F\left(x_{0}\right)\text{.}\) 于是所求积分曲线为 \(y=F(x)+\left[y_{0}-F\left(x_{0}\right)\right]\text{.}\)
Example 5.1.5.
例 1 求一条通过点 \((2,5)\text{,}\) 且切线的斜率为 \(2 x\) 的曲线方程.
Solution.
解 设所求曲线的方程为 \(y=F(x)\text{,}\) 由题意可知
\begin{equation*}
F^{\prime}(x)=2 x,
\end{equation*}
则
\begin{equation*}
F(x)=\displaystyle \int 2 x \mathrm{~d} x=x^{2}+C .
\end{equation*}
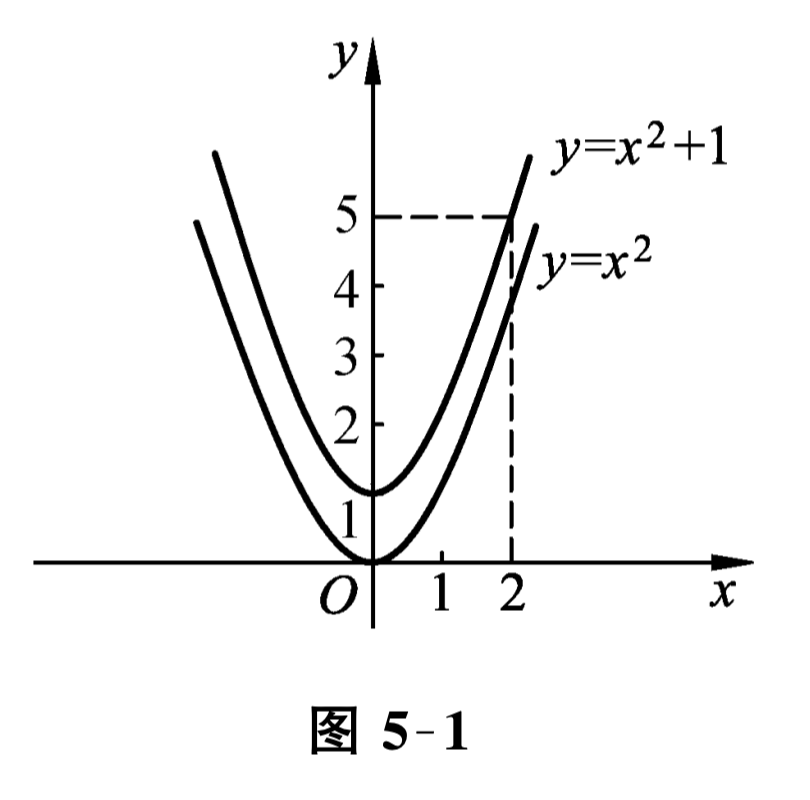
由条件可得, \(F(2)=5\) 即 \(5=2^{2}+C\text{,}\)于是 \(C=1\text{.}\)故所求曲线方程为 \(y=x^{2}+1\) (见图 5-1).
从不定积分的定义, 即可得下述关系: (1)\(\left(\displaystyle \int f(x) \mathrm{d} x\right)^{\prime}=f(x)\) 或 \(\mathrm{d}\left(\displaystyle \int f(x) \mathrm{d} x\right)=f(x) \mathrm{d} x\text{.}\) 事实上, 设 \(F(x)\) 是函数 \(f(x)\) 的一个原函数, 即 \(F^{\prime}(x)=f(x)\text{,}\) 则 \(\displaystyle \int f(x) \mathrm{d} x=\) \(F(x)+C\text{,}\) 所以
\begin{equation*}
\left(\displaystyle \int f(x) \mathrm{d} x\right)^{\prime}=(F(x)+C)^{\prime}=F^{\prime}(x)=f(x) .
\end{equation*}
(2)\(\displaystyle \int F^{\prime}(x) \mathrm{d} x=F(x)+C\) 或 \(\displaystyle \int \mathrm{d} F(x)=F(x)+C\text{.}\) 事实上, 因为 \(F(x)\) 是 \(F^{\prime}(x)\) 的原函数, 故有 \(\displaystyle \int F^{\prime}(x) \mathrm{d} x=F(x)+C\text{.}\) 求不定积分的方法称为积分法, 上式表明积分法是微分法的逆运算,因此可以利用导数公式得到基本积分公式.
Subsection 5.1.3 基本积分表
由于积分运算是微分运算的逆运算, 因此从每个基本微分公式很自然地得出相应的积分公式. 下面列出一些基本积分公式, 通常称其为基本积分表.
(1)\(\displaystyle \int k \mathrm{~d} x=k x+C\) ( \(k\) 为常数);
(2)\(\displaystyle \int x^{\alpha} \mathrm{d} x=\frac{1}{\alpha+1} x^{\alpha+1}+C(\alpha \neq-1)\text{;}\)
(3)\(\displaystyle \int \frac{1}{x} \mathrm{~d} x=\ln |x|+C\text{;}\)
(4)\(\displaystyle \int \frac{\mathrm{d} x}{1+x^{2}}=\arctan x+C\text{;}\)
(5)\(\displaystyle \int \frac{\mathrm{d} x}{\sqrt{1-x^{2}}}=\arcsin x+C\text{;}\)
(6)\(\displaystyle \int \cos x \mathrm{~d} x=\sin x+C\text{;}\)
(7)\(\displaystyle \int \sin x \mathrm{~d} x=-\cos x+C\text{;}\)
(8)\(\displaystyle \int \sec ^{2} x \mathrm{~d} x=\tan x+C\text{;}\)
(9)\(\displaystyle \int \csc ^{2} x \mathrm{~d} x=-\cot x+C\text{;}\)
(10)\(\displaystyle \int \sec x \tan x \mathrm{~d} x=\sec x+C\text{;}\)
(11)\(\displaystyle \int \csc x \cot x \mathrm{~d} x=-\csc x+C\text{;}\)
(12)\(\displaystyle \int \mathrm{e}^{x} \mathrm{~d} x=\mathrm{e}^{x}+C\text{;}\)
(13)\(\displaystyle \int a^{x} \mathrm{~d} x=\frac{a^{x}}{\ln a}+C(a>0, a \neq 1)\text{;}\)
(14)\(\displaystyle \int \operatorname{sh} x \mathrm{~d} x=\operatorname{ch} x+C\text{;}\)
(15)\(\displaystyle \int \operatorname{ch} x \mathrm{~d} x=\operatorname{sh} x+C\text{.}\)
关于公式 \(\displaystyle \int \frac{1}{x} \mathrm{~d} x=\ln |x|+C\) 作如下说明:
当 \(x>0\) 时, \((\ln x)^{\prime}=\frac{1}{x}, \displaystyle \int \frac{1}{x} \mathrm{~d} x=\ln x+C\) 则成立;
当 \(x<0\) 时, \([\ln (-x)]^{\prime}=\frac{1}{x}, \displaystyle \int \frac{1}{x} \mathrm{~d} x=\ln (-x)+C\) 则成立.
因此对任意 \(x \neq 0, \displaystyle \int \frac{1}{x} \mathrm{~d} x=\ln |x|+C\text{.}\)
Example 5.1.6.
例 2 求 \(\displaystyle \int \frac{1}{x^{4}} \mathrm{~d} x\text{.}\)
Solution.
解 \(\displaystyle \int \frac{1}{x^{4}} \mathrm{~d} x=\displaystyle \int x^{-4} \mathrm{~d} x=\frac{x^{-4+1}}{-4+1}+C=-\frac{1}{3 x^{3}}+C\text{.}\)
Example 5.1.7.
例 3 求 \(\displaystyle \int x^{2} \sqrt[3]{x} \mathrm{~d} x\text{.}\)
Solution.
解 \(\displaystyle \int x^{2} \sqrt[3]{x} \mathrm{~d} x=\displaystyle \int x^{\frac{7}{3}} \mathrm{~d} x=\frac{x^{\frac{7}{3}+1}}{\frac{7}{3}+1}+C=\frac{3}{10} x^{\frac{10}{3}}+C\text{.}\)
Example 5.1.8.
例 4 求 \(\displaystyle \int \frac{1}{\sqrt{\sqrt{x}}} \mathrm{~d} x\text{.}\)
Solution.
解 \(\displaystyle \int \frac{1}{\sqrt{\sqrt{x}}} \mathrm{~d} x=\displaystyle \int x^{-\frac{1}{4}} \mathrm{~d} x=\frac{x^{-\frac{1}{4}+1}}{-\frac{1}{4}+1}+C=\frac{4}{3} x^{\frac{3}{4}}+C\text{.}\)
上面三个例子的被积函数经整理后其实都是幂函数,遇此情形,应先把被积函数化为 \(x^{\alpha}\) 的形式, 然后应用幂函数的积分公式来求不定积分. 有了上述基本积分公式, 就可以求出基本初等函数的不定积分, 所以必须牢牢记住这些基本积分公式. 为了更好地求初等函数的不定积分, 还需要学习积分运算法则及求不定积分的各种方法.
Subsection 5.1.4 基本积分运算法则
由不定积分的定义,易证下列不定积分的运算法则. 本节中假设 \(f(x), g(x)\)的原函数都存在.
Proposition 5.1.9.
法则1 \(\displaystyle\displaystyle \int k f(x) \mathrm{d} x=k \displaystyle \int f(x) \mathrm{d} x\text{,}\) 其中 \(k\) 是常数 \((k \neq 0)\text{.}\)
即被积函数的常数因子可以移到积分号外边. 事实上, \(\left[k \displaystyle \int f(x) \mathrm{d} x\right]^{\prime}=k f(x)\text{,}\) 即 \(\displaystyle \int k f(x) \mathrm{d} x=k \displaystyle \int f(x) \mathrm{d} x\text{.}\)
Proposition 5.1.10.
法则2 \(2 \displaystyle \int[f(x) \pm g(x)] \mathrm{d} x=\displaystyle \int f(x) \mathrm{d} x \pm \displaystyle \int g(x) \mathrm{d} x\text{.}\)
事实上, \(\left[\displaystyle \int f(x) \mathrm{d} x \pm \displaystyle \int g(x) \mathrm{d} x\right]^{\prime}=\left[\displaystyle \int f(x) \mathrm{d} x\right]^{\prime} \pm\left[\displaystyle \int g(x) \mathrm{d} x\right]^{\prime}=f(x) \pm g(x)\text{.}\) 则
\begin{equation*}
\displaystyle \int[f(x) \pm g(x)] \mathrm{d} x=\displaystyle \int f(x) \mathrm{d} x \pm \displaystyle \int g(x) \mathrm{d} x
\end{equation*}
\begin{equation*}
\displaystyle \int\left[k_{1} f(x) \pm k_{2} g(x)\right] \mathrm{d} x=k_{1} \displaystyle \int f(x) \mathrm{d} x \pm k_{2} \displaystyle \int g(x) \mathrm{d} x
\end{equation*}
其中 \(k_{1}, k_{2}\) 均是非零常数. 这一运算法则可以推广到有限个函数的情况.
\begin{equation*}
\begin{aligned}
& \displaystyle \int\left[k_{1} f_{1}(x) \pm k_{2} f_{2}(x) \pm \cdots \pm k_{m} f_{m}(x)\right] \mathrm{d} x \\
= & k_{1} \displaystyle \int f_{1}(x) \mathrm{d} x \pm k_{2} \displaystyle \int f_{2}(x) \mathrm{d} x \pm \cdots \pm k_{m} \displaystyle \int f_{m}(x) \mathrm{d} x,
\end{aligned}
\end{equation*}
其中 \(k_{1}, k_{2}, \cdots, k_{m}\) 均是非零常数.
Example 5.1.11.
例 5 计算 \(\displaystyle \int\left(3^{x} \mathrm{e}^{x}+2 x^{-2}\right) \mathrm{d} x\text{.}\)
Solution.
解 \(\displaystyle \int\left(3^{x} \mathrm{e}^{x}+2 x^{-2}\right) \mathrm{d} x=\displaystyle \int(3 \mathrm{e})^{x} \mathrm{~d} x+2 \displaystyle \int x^{-2} \mathrm{~d} x=\frac{3^{x} \mathrm{e}^{x}}{1+\ln 3}-\frac{2}{x}+C\text{.}\)
Example 5.1.12.
例 6 计算 \(\displaystyle \int\left(1-\frac{1}{x^{2}}\right) \sqrt{x \sqrt{x}} \mathrm{~d} x\text{.}\)
Solution.
解 \(\displaystyle \int\left(1-\frac{1}{x^{2}}\right) \sqrt{x \sqrt{x}} \mathrm{~d} x=\displaystyle \int \sqrt{x \sqrt{x}} \mathrm{~d} x-\displaystyle \int \frac{1}{x^{2}} \sqrt{x \sqrt{x}} \mathrm{~d} x\)
\begin{equation*}
=\displaystyle \int x^{\frac{3}{4}} \mathrm{~d} x-\displaystyle \int x^{-\frac{5}{4}} \mathrm{~d} x=\frac{4}{7} x^{\frac{7}{4}}+4 x^{-\frac{1}{4}}+C .
\end{equation*}
Example 5.1.13.
例 7 计算 \(\displaystyle \int\left(5 \cos x+2-3 x^{2}+\frac{1}{x}-\frac{4}{1+x^{2}}\right) \mathrm{d} x\text{.}\)
Solution.
解 \(\displaystyle \int\left(5 \cos x+2-3 x^{2}+\frac{1}{x}-\frac{4}{1+x^{2}}\right) \mathrm{d} x\)
\begin{equation*}
\begin{aligned}
& =5 \displaystyle \int \cos x \mathrm{~d} x+2 \displaystyle \int \mathrm{d} x-3 \displaystyle \int x^{2} \mathrm{~d} x+\displaystyle \int \frac{1}{x} \mathrm{~d} x-4 \displaystyle \int \frac{1}{1+x^{2}} \mathrm{~d} x \\
& =5 \sin x+2 x-x^{3}+\ln |x|-4 \arctan x+C .
\end{aligned}
\end{equation*}
Example 5.1.14.
例 8 计算 \(\displaystyle \int\left(10^{x}+3 \sin x+\sqrt{x}\right) \mathrm{d} x\text{.}\)
Solution.
解 \(\displaystyle \int\left(10^{x}+3 \sin x+\sqrt{x}\right) \mathrm{d} x=\displaystyle \int 10^{x} \mathrm{~d} x+3 \displaystyle \int \sin x \mathrm{~d} x+\displaystyle \int \sqrt{x} \mathrm{~d} x\)
\begin{equation*}
\begin{aligned}
& =\frac{10^{x}}{\ln 10}-3 \cos x+\frac{1}{\frac{1}{2}+1} x^{\frac{1}{2}+1}+C \\
& =\frac{10^{x}}{\ln 10}-3 \cos x+\frac{2}{3} x^{\frac{3}{2}}+C .
\end{aligned}
\end{equation*}
Example 5.1.15.
例 9 计算 \(\displaystyle \int \frac{\cos 2 x}{\cos x+\sin x} \mathrm{~d} x\text{.}\)
Solution.
解 \(\displaystyle \int \frac{\cos 2 x}{\cos x+\sin x} \mathrm{~d} x=\displaystyle \int \frac{\cos ^{2} x-\sin ^{2} x}{\cos x+\sin x} \mathrm{~d} x=\displaystyle \int(\cos x-\sin x) \mathrm{d} x\)
\begin{equation*}
=\displaystyle \int \cos x \mathrm{~d} x-\displaystyle \int \sin x \mathrm{~d} x=\sin x+\cos x+C
\end{equation*}
Example 5.1.16.
例 10 计算 \(\displaystyle \int \frac{x^{4}}{1+x^{2}} \mathrm{~d} x\text{.}\)
Solution.
解 \(\displaystyle \int \frac{x^{4}}{1+x^{2}} \mathrm{~d} x=\displaystyle \int \frac{x^{4}-1+1}{1+x^{2}} \mathrm{~d} x=\displaystyle \int \frac{\left(x^{2}-1\right)\left(x^{2}+1\right)+1}{1+x^{2}} \mathrm{~d} x\)
\begin{equation*}
\begin{aligned}
& =\displaystyle \int\left(x^{2}-1+\frac{1}{1+x^{2}}\right) \mathrm{d} x=\displaystyle \int x^{2} \mathrm{~d} x-\displaystyle \int \mathrm{d} x+\displaystyle \int \frac{1}{1+x^{2}} \mathrm{~d} x \\
& =\frac{x^{3}}{3}-x+\arctan x+C .
\end{aligned}
\end{equation*}
Example 5.1.17.
例 11 计算
\begin{equation*}
\displaystyle \int \frac{1}{\sin ^{2} \frac{x}{2} \cos ^{2} \frac{x}{2}} \mathrm{~d} x
\end{equation*}
Solution.
解 \(\displaystyle \int \frac{1}{\sin ^{2} \frac{x}{2} \cos ^{2} \frac{x}{2}} \mathrm{~d} x=\displaystyle \int \frac{1}{\left(\frac{\sin x}{2}\right)^{2}} \mathrm{~d} x=4 \displaystyle \int \csc ^{2} x \mathrm{~d} x=-4 \cot x+C\text{.}\)
Example 5.1.18.
例 12 计算 \(\displaystyle \int \cos ^{2} \frac{x}{2} \mathrm{~d} x\text{.}\)
Solution.
解 \(\displaystyle \int \cos ^{2} \frac{x}{2} \mathrm{~d} x=\displaystyle \int \frac{1+\cos x}{2} \mathrm{~d} x=\frac{1}{2}\left(\displaystyle \int \mathrm{d} x+\displaystyle \int \cos x \mathrm{~d} x\right)=\frac{1}{2}(x+\sin x)+C\text{.}\)
上述各例,都是通过基本运算手段,如恒等变形、加项减项等方法求不定积分, 目的是将较复杂的被积函数简化,使之成为若干个可查基本积分表的不定积分或已知不定积分的形式.